[선형대수학] 정의, 행렬, 벡터,

이 글(선형대수학)은 유튜브에서 휴펜하임의 강의를 듣고 생각한 글이라 내용에 오류가 있을 수 있습니다.

선형 대수학이란 무엇입니까?

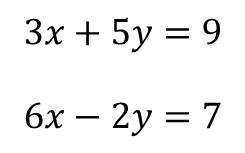
위의 선형방정식을 행렬과 벡터를 이용하여 아래와 같이 표현하는 수학을 선형대수학이라고 합니다. 다양한 방정식은 평면의 형태로 선형적으로 표현되며, 대수학의 의미는 평면의 행렬이 아닌 수학으로 표현됩니다.

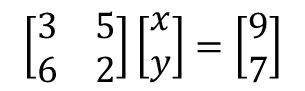
행렬, 벡터 및 연립 선형 방정식이란 무엇입니까?

먼저 선형방정식이란 수학식 1과 같은 선형방정식을 이용하여 x, y와 같은 변수값을 구하는 방정식을 의미한다.

행렬과 벡터는 기본을 정의할 생각 없이 속성으로 요약하면 다음과 같다.

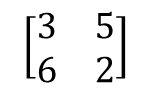
위와 같이 행렬을 행렬이라고 하며 가로축을 행으로, 세로축을 열로 표현한다.

벡터는 수학식 2의 수들이 하나로 합쳐진 형태이며, 1 x X 또는 X x 1의 형태를 벡터라고 한다.

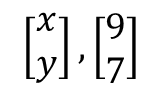
상기 수학식 2의 값이 벡터값이 된다.

벡터의 속성

벡터에는 크기와 방향이 있습니다.

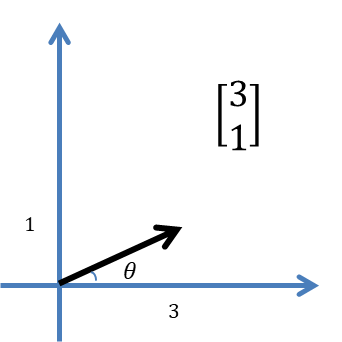
벡터는 그림 1과 같이 좌표계로 표현할 수 있습니다. 좌표계로 표현하면 그림과 같이 검정색 화살표의 길이가 크기가 되고 화살표의 방향이 벡터의 방향이 됩니다.

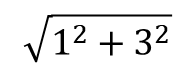
크기는 방정식 3과 같이 얻을 수 있습니다.

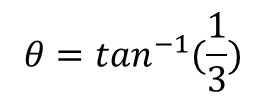
방향은 좌표에서 검은색 화살표의 각도로 결정됩니다. 따라서 위와 같이 역 탄젠트를 사용할 수 있습니다.

벡터 더하기 빼기

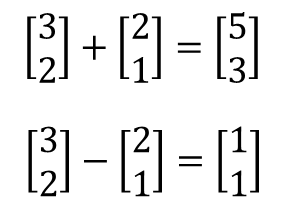
벡터 덧셈과 뺄셈은 일반 수학처럼 취급할 수 있습니다. 동일한 행과 열의 값에 더하거나 빼야 합니다.

좌표에서 벡터 값을 더하거나 빼서 만든 화살표는 결국 원점에서 화살표와 같은 값을 표시하게 됩니다.

벡터 x 내적

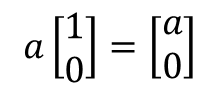
스칼라는 벡터 형식이 아닌 크기만 있는 값입니다. 벡터에 스칼라를 곱하면 벡터의 각 요소에 스칼라 값이 곱해집니다.

위 수학식 4에서 벡터의 원소는 스칼라 값에 따라 모든 원소를 표현할 수 있다.

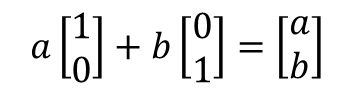
위와 같이 벡터의 모든 요소에 각각 스칼라 a와 b를 곱하면 좌표평면의 모든 값은 a와 b를 피팅하여 표현할 수 있습니다.